
\(C = 0.0 + 0.0i\)

\(C = -0.61 + 0.0i\)

\(C = 0.33 + 0.0i\)

\(C = 0.33 + 0.5i\)
Julia set is a set of complex numbers that is studied in the field of complex dynamics.
It is defined by a function \(f(z) = Z^2 + C\) of complex domain, where \(Z\) is current point in the plane and \(C\) is a hyper parameter that changes the behaviour of the system.
We compute the set by testing for every point on a plane if that point \(Z\) "converges" towards some other point (in other words it remains "bounded") or "diverges" towards infinity after \(n\) iterations. Points that remain bounded are part of the Julia set.

\(C = 0.0 + 0.0i\)

\(C = -0.61 + 0.0i\)

\(C = 0.33 + 0.0i\)

\(C = 0.33 + 0.5i\)
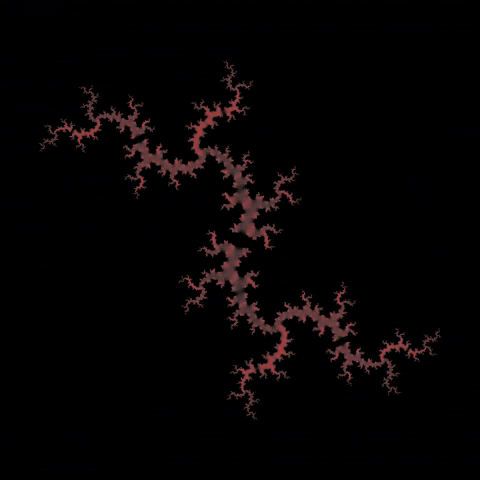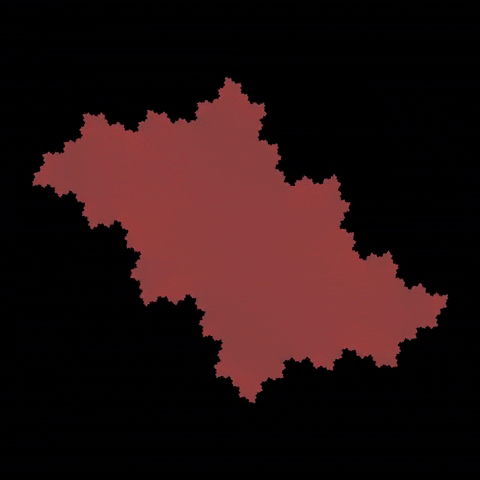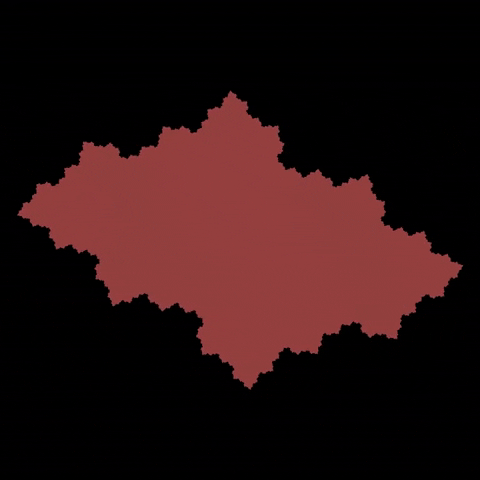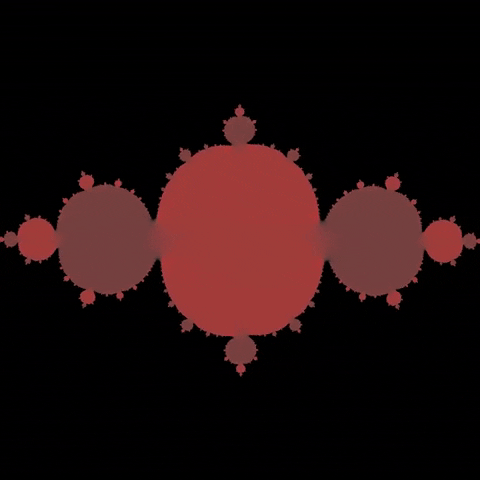


\(C = 0.61 + 0.52i\)
\(C = 0.35 + 0.04i\)

\(C = 0.44 + 0.34i\)

\(C = -0.65 + 0.04i\)

\(C = -0.65 + 0.04i\)